


Next: Detector Performance
Up: Performance
Previous: Wavelength Scale
The instrument sensitivity for full-aperture observations was
determined by comparing observations of the
hot DA white dwarf HZ 43 with the model atmosphere for this star
calculated by one of us (DF), using D. Koester's
model atmosphere codes ([Koester, Schulz, & Weidemann 1979]; [Finley, Koester, & Basri 1995]).
The parameters for this model are
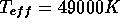 , log g = 8.0, and V = 12.91.
, log g = 8.0, and V = 12.91.
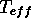 and log g were determined from fits to Balmer line profiles
(Finley, Koester, & Basri 1995), while the V magnitude was measured
by the FOS ([Bohlin, Colina, & Finley 1995]).
The models incorporate the Hummer-Mihalas occupation probability formalism
([Hummer & Mihalas 1988]) with the critical field strength parameter set to
twice the nominal value ([]).
The model was corrected for transmission through
the interstellar medium, assuming a hydrogen column density of
and log g were determined from fits to Balmer line profiles
(Finley, Koester, & Basri 1995), while the V magnitude was measured
by the FOS ([Bohlin, Colina, & Finley 1995]).
The models incorporate the Hummer-Mihalas occupation probability formalism
([Hummer & Mihalas 1988]) with the critical field strength parameter set to
twice the nominal value ([]).
The model was corrected for transmission through
the interstellar medium, assuming a hydrogen column density of
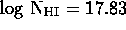 and b = 10 km s
and b = 10 km s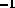 .
Extinction by dust was assumed
to be negligible. The resulting model flux was then convolved with a
gaussian of 3 Å FWHM to simulate the instrumental resolution.
.
Extinction by dust was assumed
to be negligible. The resulting model flux was then convolved with a
gaussian of 3 Å FWHM to simulate the instrumental resolution.
HZ 43 was observed three times during the mission (at 35, 64, and 329
hours MET). The last pointing contained the longest periods of
clean photometric data, and was therefore used to define the effective
area. Following acquisition, a 470 s integration was obtained through
the 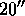 round slit, followed by a 696 s integration through the
round slit, followed by a 696 s integration through the
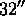 round slit; both integrations were entirely within orbital night.
The observed count rates were the same for the two integrations, and
the count rate fluctuations on a two second time scale are consistent
with Poisson noise, indicating that both portions of the observation
are photometric. We therefore combined the two spectra, and applied the following corrections:
(1) Pulse pile-up: This is event loss caused by the arrival
of overlapping events on the photodiode array within the 1 msec readout time;
this effect and the correction scheme are described
in [Kruk95].
The peak correction is 9% at 1085 Å, dropping to
round slit; both integrations were entirely within orbital night.
The observed count rates were the same for the two integrations, and
the count rate fluctuations on a two second time scale are consistent
with Poisson noise, indicating that both portions of the observation
are photometric. We therefore combined the two spectra, and applied the following corrections:
(1) Pulse pile-up: This is event loss caused by the arrival
of overlapping events on the photodiode array within the 1 msec readout time;
this effect and the correction scheme are described
in [Kruk95].
The peak correction is 9% at 1085 Å, dropping to  1% at
either end of the spectrum.
(2) Dark count subtraction: 0.01%--0.1%; see § 3.5.
(3) Scattered light subtraction: 0.005--0.1%; also see § 3.5.
(4) Second order subtraction: the equivalent of 21% of the counts Å
1% at
either end of the spectrum.
(2) Dark count subtraction: 0.01%--0.1%; see § 3.5.
(3) Scattered light subtraction: 0.005--0.1%; also see § 3.5.
(4) Second order subtraction: the equivalent of 21% of the counts Å 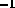 in the 912--920 Å region contribute in second order at
1824--1840 Å. This excess is subtracted from the data.
The extreme-ultraviolet (EUV) flux (< 912 Å) appearing in second order
is estimated to peak at about 1% of the counts at 1550 Å, drop to 0.5%
at 1300 Å and 1650 Å
and drop rapidly to zero shortward of Lyman
in the 912--920 Å region contribute in second order at
1824--1840 Å. This excess is subtracted from the data.
The extreme-ultraviolet (EUV) flux (< 912 Å) appearing in second order
is estimated to peak at about 1% of the counts at 1550 Å, drop to 0.5%
at 1300 Å and 1650 Å
and drop rapidly to zero shortward of Lyman  .
This EUV flux was ignored in the present calibration, but will be included
in future revisions.
(5) Flat field corrections: see § 3.4.
(6) Time dependence of the instrument throughput: see below.
.
This EUV flux was ignored in the present calibration, but will be included
in future revisions.
(5) Flat field corrections: see § 3.4.
(6) Time dependence of the instrument throughput: see below.
To produce the instrument sensitivity curve we divided the
corrected count spectrum into the model flux spectrum.
Dividing this into the energy per photon as a function of wavelength and
dividing by the (slightly variable) pixel width gives the effective
area, which is shown in Figure 2. The peak
effective area is 24.1 cm at 1160 Å, where the
corresponding inverse sensitivity is
at 1160 Å, where the
corresponding inverse sensitivity is 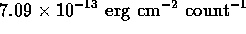 . For comparison, we also
show the final effective area curve for the Astro-1 version of HUT
([Kruk95]). As was the case on Astro-1, the effective area
measured in-flight is in fairly good agreement with the pre-flight
laboratory calibration shortward of
. For comparison, we also
show the final effective area curve for the Astro-1 version of HUT
([Kruk95]). As was the case on Astro-1, the effective area
measured in-flight is in fairly good agreement with the pre-flight
laboratory calibration shortward of 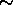 1050 Å, but
falls roughly 30% below it at longer wavelengths. This difference is
believed to be due to aging of the CsI photocathode.
1050 Å, but
falls roughly 30% below it at longer wavelengths. This difference is
believed to be due to aging of the CsI photocathode.
The stability of the instrument throughput was monitored by making
multiple observations
of the DA white dwarf GD 394 (at 64, 92, 138, 211, and 341 hours MET),
in addition to the three observations of HZ 43 listed above.
The sensitivity was found to
decline gradually over the course of the mission in a
wavelength-dependent fashion.
The total decline was relatively small at long wavelengths
(5% at 1800 Å), and rose steadily towards shorter wavelengths
(27% at 912 Å). The rate of decline was greatest early in the mission,
with roughly half of the total decline occurring prior to 100 hours MET,
and 75% of the total decline occurring by 138 hours MET.
A family of correction curves was calculated by fitting three-term
Chebyshev polynomials to the ratios of late to early observations of
HZ 43 and GD 394.
These correction factors are shown in Figure 3.
A correction curve for any given MET can be
obtained by interpolating among the curves.
Neither the wavelength dependence nor the time dependence of this degradation
matches that of the detector exposure: the total flux per unit area on
the detector has a broad maximum over 1100--1350 Å and drops rapidly
towards either end of the detector, and it increases with time during the
mission
primarily during observations of a relatively small number of bright stars.
Both, however, are consistent with
possible degradation of the primary mirror. Two possible mechanisms for
this are condensation of contaminants onto the mirror, and oxidation of
the SiC coating by energetic atomic oxygen. One of the witness mirrors
removed from the telescope shortly after the flight shows similar
degradation, and is being investigated further.
An internal consistency check on the white dwarf models and on our data
reduction procedures can be made by comparing the observed flux with
the model predictions for other hot DA white dwarf stars spanning
a range of effective temperatures and surface gravities. We observed
GD 71, GD 153, RE 0512--004, GD 50, Wolf 1346, and RE 1738+669 through
the full aperture as part of the Guest Investigator program of D. Finley,
D. Koester, and R. Kimble.
These spectra were reduced and compared with models in the same manner
as described above for HZ 43.
As shown in Figure 4,
for GD 71, GD 153, RE 0512--004, and GD 50 the
observed spectra agree with the models to better than 5%.
The parameters for the models shown are:
GD 71: 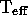 = 32300 K, log g = 7.73, V = 13.032;
GD 153:
= 32300 K, log g = 7.73, V = 13.032;
GD 153: 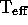 = 38500 K, log g = 7.67, V = 13.353;
RE 0512--004:
= 38500 K, log g = 7.67, V = 13.353;
RE 0512--004: 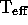 = 32000 K, log g = 7.4, V = 13.80;
and GD 50:
= 32000 K, log g = 7.4, V = 13.80;
and GD 50: 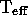 = 41000 K, log g = 9.2, V = 14.00.
All of the model parameters were derived from fits to Balmer line
profiles and from V-band photometry ([Finley, Koester, & Basri 1995]).
For Wolf 1346 the observed spectrum agrees with the model
to within measurement errors, except for wavelengths 1080--1150 Å\
(between the broad merging absorption wings of Lyman
= 41000 K, log g = 9.2, V = 14.00.
All of the model parameters were derived from fits to Balmer line
profiles and from V-band photometry ([Finley, Koester, & Basri 1995]).
For Wolf 1346 the observed spectrum agrees with the model
to within measurement errors, except for wavelengths 1080--1150 Å\
(between the broad merging absorption wings of Lyman  and
Lyman
and
Lyman 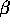 ), where the data exceed the model by as much as 18%.
The observed flux for RE 1738+669 is consistent with the IUE flux;
comparisons with the model flux will require corrections for interstellar
extinction and molecular hydrogen that are still in progress.
), where the data exceed the model by as much as 18%.
The observed flux for RE 1738+669 is consistent with the IUE flux;
comparisons with the model flux will require corrections for interstellar
extinction and molecular hydrogen that are still in progress.
The instrument throughput for door configurations other than fully open
was determined by taking ratios of spectra obtained through more
than one door state on the same object.
Since the various door states illuminate different
regions of the mirror, grating, and detector (and illuminate the detector
at different angles), the corresponding throughputs differ by more than
just the relative exposed areas of the mirror.
The throughput for the half--open door state was determined by obtaining
spectra of both HZ 43 and GD 153 through
both the full and half open door states. The two sets of spectra gave
essentially similar ratios of half to full door flux, so the two
ratios were averaged.
The resulting throughput ratio rises
from 0.475 at 912 Å to 0.50 at 1400 Å then declines gradually to
0.415 at 1830 Å.
The 750 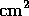 door state was calibrated by two different means:
by observing GD 394 through this door as well as through the full aperture,
and by direct observation of the hot DA white dwarf G191--B2B. The
data for G191--B2B were reduced in the same manner as described above
for HZ 43.
The model atmosphere parameters used for G191--B2B were
door state was calibrated by two different means:
by observing GD 394 through this door as well as through the full aperture,
and by direct observation of the hot DA white dwarf G191--B2B. The
data for G191--B2B were reduced in the same manner as described above
for HZ 43.
The model atmosphere parameters used for G191--B2B were
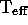 = 60000 K, log g = 7.4, and V = 11.79.
This model differs by
= 60000 K, log g = 7.4, and V = 11.79.
This model differs by 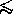 2% from that used to define the
HUT calibration for Astro-1.
In order to keep any model dependence in the calibration
the same for all door states however, the effective area curve for this
door state was determined by fitting a 2--piece cubic spline to the ratio
of the G191--B2B-derived effective area and the HZ 43-derived full aperture
effective area, and then multiplying by the full aperture effective area.
This retains the large--scale wavelength dependence of the G191--B2B
effective area determination, but should remove any additional
small--scale artifacts introduced by small errors in the model parameters,
mismatches between the model and the actual spectral resolution, etc.
The observations of GD 394 gave results that were consistent with the
G191--B2B calibration, but with considerably poorer statistics.
2% from that used to define the
HUT calibration for Astro-1.
In order to keep any model dependence in the calibration
the same for all door states however, the effective area curve for this
door state was determined by fitting a 2--piece cubic spline to the ratio
of the G191--B2B-derived effective area and the HZ 43-derived full aperture
effective area, and then multiplying by the full aperture effective area.
This retains the large--scale wavelength dependence of the G191--B2B
effective area determination, but should remove any additional
small--scale artifacts introduced by small errors in the model parameters,
mismatches between the model and the actual spectral resolution, etc.
The observations of GD 394 gave results that were consistent with the
G191--B2B calibration, but with considerably poorer statistics.
The 200  door state was also calibrated by an observation of
G191--B2B. The data reduction procedures were the same as for the
750
door state was also calibrated by an observation of
G191--B2B. The data reduction procedures were the same as for the
750  observation. The ratio of the two spectra was nearly
independent of wavelength and was equal to 0.273, quite close to the nominal
ratio of geometric areas (0.267).
observation. The ratio of the two spectra was nearly
independent of wavelength and was equal to 0.273, quite close to the nominal
ratio of geometric areas (0.267).
The 50  door state was calibrated by observing the hot sdO
star BD+75
door state was calibrated by observing the hot sdO
star BD+75 325 through both the 200
325 through both the 200 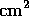 and 50
and 50 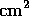 doors.
Longward of 1025 Å the ratio of the two spectra is independent
of wavelength and is equal to 0.273; shortward of 1025 Å the ratio
drops smoothly to about 0.24 at 912 Å. The effective area for the
200
doors.
Longward of 1025 Å the ratio of the two spectra is independent
of wavelength and is equal to 0.273; shortward of 1025 Å the ratio
drops smoothly to about 0.24 at 912 Å. The effective area for the
200 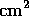 door derived from the G191--B2B measurement was scaled
by this ratio to determine the 50
door derived from the G191--B2B measurement was scaled
by this ratio to determine the 50 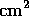 door effective area.
Since the calibration for these two door states is the furthest removed
from the HZ 43-derived full aperture calibration, a test of our data reduction
and calibration procedures can be made by comparing our spectrum for
BD+75
door effective area.
Since the calibration for these two door states is the furthest removed
from the HZ 43-derived full aperture calibration, a test of our data reduction
and calibration procedures can be made by comparing our spectrum for
BD+75 325 with that obtained by the FOS (kindly provided by
R. Bohlin).
The HUT and FOS spectra for this star are shown in
Figure 5,
for the wavelength region common to both instruments. The two spectra
agree to within 5% at most wavelengths and to within 10% everywhere.
325 with that obtained by the FOS (kindly provided by
R. Bohlin).
The HUT and FOS spectra for this star are shown in
Figure 5,
for the wavelength region common to both instruments. The two spectra
agree to within 5% at most wavelengths and to within 10% everywhere.



Next: Detector Performance
Up: Performance
Previous: Wavelength Scale
kruk@pha.jhu.edu
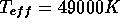 , log g = 8.0, and V = 12.91.
, log g = 8.0, and V = 12.91.
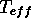 and log g were determined from fits to Balmer line profiles
(Finley, Koester, & Basri 1995), while the V magnitude was measured
by the FOS ([Bohlin, Colina, & Finley 1995]).
The models incorporate the Hummer-Mihalas occupation probability formalism
([Hummer & Mihalas 1988]) with the critical field strength parameter set to
twice the nominal value ([]).
The model was corrected for transmission through
the interstellar medium, assuming a hydrogen column density of
and log g were determined from fits to Balmer line profiles
(Finley, Koester, & Basri 1995), while the V magnitude was measured
by the FOS ([Bohlin, Colina, & Finley 1995]).
The models incorporate the Hummer-Mihalas occupation probability formalism
([Hummer & Mihalas 1988]) with the critical field strength parameter set to
twice the nominal value ([]).
The model was corrected for transmission through
the interstellar medium, assuming a hydrogen column density of
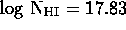 and b = 10 km s
and b = 10 km s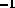 .
Extinction by dust was assumed
to be negligible. The resulting model flux was then convolved with a
gaussian of 3 Å FWHM to simulate the instrumental resolution.
.
Extinction by dust was assumed
to be negligible. The resulting model flux was then convolved with a
gaussian of 3 Å FWHM to simulate the instrumental resolution.



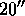 round slit, followed by a 696 s integration through the
round slit, followed by a 696 s integration through the
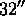 round slit; both integrations were entirely within orbital night.
The observed count rates were the same for the two integrations, and
the count rate fluctuations on a two second time scale are consistent
with Poisson noise, indicating that both portions of the observation
are photometric. We therefore combined the two spectra, and applied the following corrections:
(1) Pulse pile-up: This is event loss caused by the arrival
of overlapping events on the photodiode array within the 1 msec readout time;
this effect and the correction scheme are described
in [
round slit; both integrations were entirely within orbital night.
The observed count rates were the same for the two integrations, and
the count rate fluctuations on a two second time scale are consistent
with Poisson noise, indicating that both portions of the observation
are photometric. We therefore combined the two spectra, and applied the following corrections:
(1) Pulse pile-up: This is event loss caused by the arrival
of overlapping events on the photodiode array within the 1 msec readout time;
this effect and the correction scheme are described
in [ 1% at
either end of the spectrum.
(2) Dark count subtraction: 0.01%--0.1%; see § 3.5.
(3) Scattered light subtraction: 0.005--0.1%; also see § 3.5.
(4) Second order subtraction: the equivalent of 21% of the counts Å
1% at
either end of the spectrum.
(2) Dark count subtraction: 0.01%--0.1%; see § 3.5.
(3) Scattered light subtraction: 0.005--0.1%; also see § 3.5.
(4) Second order subtraction: the equivalent of 21% of the counts Å 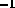 in the 912--920 Å region contribute in second order at
1824--1840 Å. This excess is subtracted from the data.
The extreme-ultraviolet (EUV) flux (< 912 Å) appearing in second order
is estimated to peak at about 1% of the counts at 1550 Å, drop to 0.5%
at 1300 Å and 1650 Å
and drop rapidly to zero shortward of Lyman
in the 912--920 Å region contribute in second order at
1824--1840 Å. This excess is subtracted from the data.
The extreme-ultraviolet (EUV) flux (< 912 Å) appearing in second order
is estimated to peak at about 1% of the counts at 1550 Å, drop to 0.5%
at 1300 Å and 1650 Å
and drop rapidly to zero shortward of Lyman  .
This EUV flux was ignored in the present calibration, but will be included
in future revisions.
(5) Flat field corrections: see § 3.4.
(6) Time dependence of the instrument throughput: see below.
.
This EUV flux was ignored in the present calibration, but will be included
in future revisions.
(5) Flat field corrections: see § 3.4.
(6) Time dependence of the instrument throughput: see below.
 at 1160 Å, where the
corresponding inverse sensitivity is
at 1160 Å, where the
corresponding inverse sensitivity is 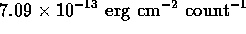 . For comparison, we also
show the final effective area curve for the Astro-1 version of HUT
([
. For comparison, we also
show the final effective area curve for the Astro-1 version of HUT
([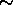 1050 Å, but
falls roughly 30% below it at longer wavelengths. This difference is
believed to be due to aging of the CsI photocathode.
1050 Å, but
falls roughly 30% below it at longer wavelengths. This difference is
believed to be due to aging of the CsI photocathode.
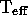 = 32300 K, log g = 7.73, V = 13.032;
GD 153:
= 32300 K, log g = 7.73, V = 13.032;
GD 153: 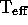 = 38500 K, log g = 7.67, V = 13.353;
RE 0512--004:
= 38500 K, log g = 7.67, V = 13.353;
RE 0512--004: 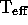 = 32000 K, log g = 7.4, V = 13.80;
and GD 50:
= 32000 K, log g = 7.4, V = 13.80;
and GD 50: 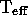 = 41000 K, log g = 9.2, V = 14.00.
All of the model parameters were derived from fits to Balmer line
profiles and from V-band photometry ([
= 41000 K, log g = 9.2, V = 14.00.
All of the model parameters were derived from fits to Balmer line
profiles and from V-band photometry ([ and
Lyman
and
Lyman 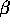 ), where the data exceed the model by as much as 18%.
The observed flux for RE 1738+669 is consistent with the IUE flux;
comparisons with the model flux will require corrections for interstellar
extinction and molecular hydrogen that are still in progress.
), where the data exceed the model by as much as 18%.
The observed flux for RE 1738+669 is consistent with the IUE flux;
comparisons with the model flux will require corrections for interstellar
extinction and molecular hydrogen that are still in progress.
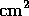 door state was calibrated by two different means:
by observing GD 394 through this door as well as through the full aperture,
and by direct observation of the hot DA white dwarf G191--B2B. The
data for G191--B2B were reduced in the same manner as described above
for HZ 43.
The model atmosphere parameters used for G191--B2B were
door state was calibrated by two different means:
by observing GD 394 through this door as well as through the full aperture,
and by direct observation of the hot DA white dwarf G191--B2B. The
data for G191--B2B were reduced in the same manner as described above
for HZ 43.
The model atmosphere parameters used for G191--B2B were
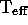 = 60000 K, log g = 7.4, and V = 11.79.
This model differs by
= 60000 K, log g = 7.4, and V = 11.79.
This model differs by 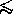 2% from that used to define the
HUT calibration for Astro-1.
In order to keep any model dependence in the calibration
the same for all door states however, the effective area curve for this
door state was determined by fitting a 2--piece cubic spline to the ratio
of the G191--B2B-derived effective area and the HZ 43-derived full aperture
effective area, and then multiplying by the full aperture effective area.
This retains the large--scale wavelength dependence of the G191--B2B
effective area determination, but should remove any additional
small--scale artifacts introduced by small errors in the model parameters,
mismatches between the model and the actual spectral resolution, etc.
The observations of GD 394 gave results that were consistent with the
G191--B2B calibration, but with considerably poorer statistics.
2% from that used to define the
HUT calibration for Astro-1.
In order to keep any model dependence in the calibration
the same for all door states however, the effective area curve for this
door state was determined by fitting a 2--piece cubic spline to the ratio
of the G191--B2B-derived effective area and the HZ 43-derived full aperture
effective area, and then multiplying by the full aperture effective area.
This retains the large--scale wavelength dependence of the G191--B2B
effective area determination, but should remove any additional
small--scale artifacts introduced by small errors in the model parameters,
mismatches between the model and the actual spectral resolution, etc.
The observations of GD 394 gave results that were consistent with the
G191--B2B calibration, but with considerably poorer statistics.
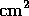 door state was also calibrated by an observation of
G191--B2B. The data reduction procedures were the same as for the
750
door state was also calibrated by an observation of
G191--B2B. The data reduction procedures were the same as for the
750 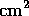 observation. The ratio of the two spectra was nearly
independent of wavelength and was equal to 0.273, quite close to the nominal
ratio of geometric areas (0.267).
observation. The ratio of the two spectra was nearly
independent of wavelength and was equal to 0.273, quite close to the nominal
ratio of geometric areas (0.267).
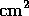 door state was calibrated by observing the hot sdO
star BD+75
door state was calibrated by observing the hot sdO
star BD+75 325 through both the 200
325 through both the 200 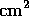 and 50
and 50 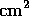 doors.
Longward of 1025 Å the ratio of the two spectra is independent
of wavelength and is equal to 0.273; shortward of 1025 Å the ratio
drops smoothly to about 0.24 at 912 Å. The effective area for the
200
doors.
Longward of 1025 Å the ratio of the two spectra is independent
of wavelength and is equal to 0.273; shortward of 1025 Å the ratio
drops smoothly to about 0.24 at 912 Å. The effective area for the
200 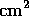 door derived from the G191--B2B measurement was scaled
by this ratio to determine the 50
door derived from the G191--B2B measurement was scaled
by this ratio to determine the 50 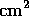 door effective area.
Since the calibration for these two door states is the furthest removed
from the HZ 43-derived full aperture calibration, a test of our data reduction
and calibration procedures can be made by comparing our spectrum for
BD+75
door effective area.
Since the calibration for these two door states is the furthest removed
from the HZ 43-derived full aperture calibration, a test of our data reduction
and calibration procedures can be made by comparing our spectrum for
BD+75 325 with that obtained by the FOS (kindly provided by
R. Bohlin).
The HUT and FOS spectra for this star are shown in
Figure
325 with that obtained by the FOS (kindly provided by
R. Bohlin).
The HUT and FOS spectra for this star are shown in
Figure