Starting with the cross-correlation software described in ![]() 2.1.
we compared wavelengths for some 50 echelle orders in all small-aperture,
optimally exposed WAVECAL spectra (278 for LWP, 291 for LWR, and
468 for SWP) against the reference spectra used by Garhart et al. (1997)
in the ecreidentify step of their calibration. The cross-correlations
showed that the zero-point shifts found for the SWP data have the
most complicated dependences of all three cameras and, in particular, that
they exhibit fluctuations in wavelength as well as time.
An example of the dissimilar
dependences with time at different wavelengths for this camera is
depicted in Figure 1: and requires some discussion.
2.1.
we compared wavelengths for some 50 echelle orders in all small-aperture,
optimally exposed WAVECAL spectra (278 for LWP, 291 for LWR, and
468 for SWP) against the reference spectra used by Garhart et al. (1997)
in the ecreidentify step of their calibration. The cross-correlations
showed that the zero-point shifts found for the SWP data have the
most complicated dependences of all three cameras and, in particular, that
they exhibit fluctuations in wavelength as well as time.
An example of the dissimilar
dependences with time at different wavelengths for this camera is
depicted in Figure 1: and requires some discussion.
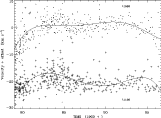 Figure 1
Figure 1
Cross-correlation shifts of 415 WAVECAL
SWP echellograms during the
lifetime of the IUE for
orders at the opposite ends of the camera, centered at 1168 Å
and 1969 Å.
In analyzing the WAVECAL data, we found that it was necessary to discard the pre-1979.0 (satellite commissioning period) SWP camera WAVECALs from further analysis because the zero-points otherwise showed a very steep increase during 1978. We then fit the shifts for the remaining sample of 415 spectra with 7th-degree polynomial both in time and echelle order. No such complications were found for the long-wavelength cameras. The cross-correlation results for all three cameras are plotted with time in Figures 2 and 3. Figure 2 was constructed by averaging the wavelength shifts such as those shown in Figure 1 over echelle orders.
Figure 2
Velocity shifts
of SWP camera WAVECAL echellograms during the IUE
lifetime. The solid line is a cubic polynomial fit (zero-point arbitrary)
which shows the (incomplete) extent to which time dependences were removed
from the WAVECAL wavelength zero points.
Note that at certain epochs the difference between an local mean and the
smooth curve may amount to ![]() 2 km s-1. Such residuals are not
removed in the wavelength calibration of NEWSIPS.
2 km s-1. Such residuals are not
removed in the wavelength calibration of NEWSIPS.
Figure 3
Wavelength-integrated cross-correlation shifts of WAVECAL echellograms
of the two IUE long-wavelength cameras
during IUE lifetime. Shifts represent wavelength
zero-point differences and are expressed as velocities. Solid line depicts
the fit with a linear (LWP) and cubic (LWR) function.
The complicated dependence of the SWP camera wavelength zero-points
as a function of time and spatial direction (echelle order) is reminiscent
of the complicated decay of this camera's ``null flux" surface with time, as
recently documented by González-Riestra (1998) and Smith (1999).
During 1979-80 the zero-point of the WAVECAL spectra increased
smoothly by ![]() +15 km s-1 (about 2 pixels) for order m = 70
(
+15 km s-1 (about 2 pixels) for order m = 70
(![]() 1170), decreased by about -4 km s-1 during the mid-1980's,
and decreased rapidly during the last 2-3 years of the mission.
For m = 118 (
1170), decreased by about -4 km s-1 during the mid-1980's,
and decreased rapidly during the last 2-3 years of the mission.
For m = 118 (![]() 1970), at the other end of the camera, the
corresponding changes in zero-point are +4.5 km s-1, 0 km s-1,
and -2 km s-1. One sees that the greatest changes occur in the
``short-wavelength" corner of the echelle surface, primarily during both
the early and late stages of the IUE mission. Since changes occurred
in the raw background flux at about the same epochs and in the same
region of the camera as the changes we report here,
it is possible that changes in the camera characteristics influenced the
positions of the echelle format as well as the net fluxes of these orders
as a function of time.
1970), at the other end of the camera, the
corresponding changes in zero-point are +4.5 km s-1, 0 km s-1,
and -2 km s-1. One sees that the greatest changes occur in the
``short-wavelength" corner of the echelle surface, primarily during both
the early and late stages of the IUE mission. Since changes occurred
in the raw background flux at about the same epochs and in the same
region of the camera as the changes we report here,
it is possible that changes in the camera characteristics influenced the
positions of the echelle format as well as the net fluxes of these orders
as a function of time.
In contrast, the WAVECAL zero-points for the long-wavelength cameras can be fit with low order polynomials, and they do not have a marked dependence on position on the detector. The LWP camera is particularly well behaved in this respect since its wavelengths (Fig. 3a) change linearly by +3 km s-1 over the interval 1980-1996.8. For the LWR camera (Fig. 3b) the wavelengths change by about +4 km s-1 during 1978-1980 and remain almost constant thereafter.
Low-order (cubic) fits for the zero-point dependences of the
WAVECALs for the three cameras were hard-coded
into NEWSIPS in order to remove such trends from the science data.
For the LWP camera data the dependence on
time is linear, so the trends could be removed completely. For the
LWR camera the removal of trends is probably very good except for fitting
the rapid increase during the first 2-3 years of the mission.
A cubic polynomial cannot fully remove this early-epoch trend.
As implied above, the complex dependence for the SWP camera
cannot be accurately fit with a cubic polynomial function, particularly
either early or late in the mission. This can be seen by comparing
the cubic fit to the shifts in Figure 2. The differences between
this line and the zero-points of the individual WAVECAL spectra imply
that, independent of other error sources, SWP data can be expected
to have small (![]() ± 2 km s-1) epoch-dependent errors.
± 2 km s-1) epoch-dependent errors.
Aside from temporal trends in the mean shifts, one can see from Figures 2 and 3 that the r.m.s. scatter characteristics of zero-points among WAVECAL spectra also change with time. Considering the SWP camera results first, Fig. 2 shows that starting sometime in 1988-90 the scatter decreased to only about 60% of its initial value of ± 2.5 km s-1. Also, the statistical outlying points (defined as those differing from the epochal mean by at least 1 pixel or 8 km-1) decreased in occurrence from over 10% of all obervations to only about 4%. It is possible that these changes are caused by the termination of adding TFLOOD lamp exposures onto the WAVECAL spectra. Other changes were made during this period, such as taking these observations under more tightly defined constraints in THDA and focus, might have contributed to the improved scatter characteristics as well. The scatter for LWR WAVECAL data seems to decrease well before 1990, so the practice of adding TFLOOD does not seem to be important. Also, notice that the scatter for the LWP camera actually seems to have increased markedly in 1990. The suddenness of this change, particularly in the LWP camera, suggests that the change in adding TFLOOD flux might have contributed to the scatter of the WAVECAL zero-points for the calibration of this camera.