Princeton University Observatory

Princeton, New Jersey

April 11, 1975

TO: Copernicus Astronomers and Guest Investigators
FROM: Edward B . Jenkins
SUBJECT: Computations of the U1 Instrumental Profile

a) Star Image

The shape of the instrumental profile for U1 has been computed under the assumption that the spectrometer is exactly in focus, the grating is perfect, the starlight illumination is uniform across the entrance slit, and no aberrations of higher order than astigmatism and coma are present. The U1 slit and the image shapes should appear as follows:

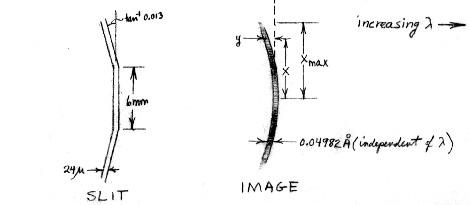
Note that the brightness of the image varies along its length; this is caused by uneven illumination of the grating. Occultation by the spectrometer and secondary spider casts a shadow on the grating which produces an intensity distribution
|x/xmax| 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
I(x) 0.00 0.30 0.29 0.28 0.88 0.83 0.76 0.67 0.55 0.40 0.10
We assume the grating efficiency and telescope mirror efficiencies are uniform over their surfaces. The above numbers represent the illumination pattern along successively higher strips, from center to edge, which are perpendicular to the rulings. (We ignore a slight asymmetry in the pattern, which makes I(x) slightly different from I(-x) for |x| ~ 0.4.)

If R is the radius of curvature of the grating (and the diameter of the Rowland circle; this value is 998.8 mm), the height L of the illumination on the grating is R(cos i)/20 for an f/20 beam with an angle of incidence i. The astigmatic image height is given by

2xmax = L Gamma

where Gamma = sin2 r + sin i tan i cos r (r is the angle of diffraction). The curvature of this image follows the relation

y = -Psi x2/2R

where

Psi = [sin i tan2i - sin r + {tan r(1- Gamma)2}/cos r] Gamma-2

For most wavelengths along the spectrum the segmented slit compensates for the curve. To ascertain the small smearing which results from the lack of a perfect match, we may define an offset

y'(x) = y(x) for |x| <= 3.0 mm

and

y'(x) = y(x) - 0.013(|x| - 3.0 mm) for |x| > 3.0 mm

If the entrance and exit slits had infinitesimal widths, we would expect an instrumental profile whose shape follows the function

P(y') = Sum (dy'/dx)-1I(x)

where the sum includes all points along the line from 0 to xmax where the function crosses y'. The conversion from y' to Delta Lambda is given by

Delta Lambda = mR/d cos r y' = 2.0858 x 103 cos r y' for y' in mm and Delta Lambda in mÅ

(m and d are the order and groove spacing, respectively). If one were to scan across any small piece of the curved image with the exit slit, one would expect to see the convolution of the two slits which results in a trapezoid,

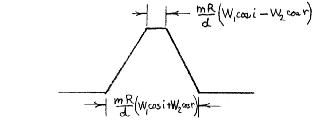mR/d W1cos i = 49.82 mÅ
(= FWHM1 at all Lambda)

where W1 and W2 are the entrance and exit slit widths, respectively.

Although the face of the exit slit is always tangent to the Rowland circle, the effective width W2 varies slightly with wavelength since the light strikes the jaws at the diffraction angle r from the normal, and the jaws are not perfectly thin. The projected widths as seen from the grating W2 cos r has been measured by Perkin-Elmer and a functional fit to these data has been made by J. B. Rogerson.

A convolution of P(Delta Lambda) with the above shown trapezoid gives us the net instrumental profile, which includes the slit widths and the small lack of registration of exit slit shape with the image curvature. Some additional smearing should be caused by spherical aberration, giving an image diameter

A =L3/(8R2) (sin i tan i + sin r tan r) cos r

which may be multiplied by 2.0858 x 103 cos r to give the value in mÅ. The above figure, however, is appropriate at the paraxial focus. The aberration may be substantially reduced (by about a factor of four, I am told), by viewing the line at the circle of least confusion, instead of the paraxial focus.

b) Diffuse Sources

If the entrance slit is illuminated uniformly over its entire length l (3.0 mm), the diffracted image is smeared vertically over a length l sec i cos r. However, for any point source off the grating centerline the displacement of the focused image is not exactly vertical, but rather occurs along an arc concave toward longer wavelengths (i.e. opposite to the curvature of the image) whose radius of curvature

re = R/Phi

where Phi = (sin i + sin r)/cos2r. For the Copernicus spectrometer actual values of re are several times larger than the radius of curvature of the image R/Psi defined earlier. The net instrumental profile for a diffuse source can be evaluated by adding together the profiles for many single point sources arranged along the entrance slit.

c) Presentation of Results

The graphs show for 950 <= Lambda <= 1400 Å, in steps of 50 Å, three computed profiles:
  1. Simple trapezoids from the slit convolutions.
  2. Profile for a star imaged on the slit center,
  3. Profile for a diffuse source illuminating the whole slit.
Because of the uncertainty of the actual focus condition of the spectrograph, no attempt was made to include the smearing from spherical aberration (we also have no firm way of knowing the effect of other sources of image blur or lack of registration). In addition to a slight broadening over (1), the mean Delta Lambda of profiles (2) and (3) are displaced (usually) toward shorter wavelengths. When the profiles were plotted, they were shifted so that their "centers of gravity" were coincident, to facilitate the comparison of shapes. The amount of these shifts for (2) and (3) in mÅ are shown as CG2 and CG3, respectively. Positive values for these quantities mean the centroid of the complete profile falls at shorter wavelengths than the simple trapezoid (on axis image). Also shown on the graphs are computed values for i, r, Gamma , Psi , Phi, and A. The values of A shows us the basic magnitude of the spherical aberration and its behavior for changing wavelengths.

It is of interest to compare the computed curves with actual observations in orbit. Two sources of information are available at present. First, W. Morton and L. Spitzer have measured stacked profiles of H2 lines which are presumed to be quite narrow. They find a good fit for the region 1025 <~ Lambda <~ 1100 Å is a gaussian profile with a FWHM = 51 mÅ. This relation is plotted as a series of dots on the 1050 Å graph, and it is evident that no really significant source of additional smearing is at work in the spectrograph, except possibly in the wings beyond | Delta Lambda | = 40 mÅ. The other main source of observational material is the stack of geocoronal Lyman Alpha emission scans. Here, however, the emission profile is not so much smaller than the instrumental profile that we may ignore its effect in producing a slightly broader profile. In connection with research on the cometary Lyman Alpha observations, J. L. Bertaux has examined the geocoronal data and has also theoretically estimated the true Lyman Alpha profile shape. The observations give an approximately gaussian profile with FWHM = 67 mÅ while the emission profile is expected to be 38 mÅ wide. We therefore would expect to find the response of our instrument to a diffuse source of Lyman Alpha of infinitesimal width in Delta Lambda to be roughly a gaussian with FWHM = (672-382)½ = 55 mÅ. The computed curve at 1200 Å has FWHM = 60 mÅ; perhaps the geocoronal emission width was overestimated by Bertaux or else the difference may be attributable to the fact that the instrumental profile is not really a pure gaussian distribution.

References

Texts which discuss in some detail the aberrations mentioned in the beginning of this writeup are as follows:

Samson, J. A. 1967, Techniques of Vacuum Ultraviolet Spectroscopy (Wiley, New York) pp. 5-19.

Welford, W. T. 1965, in Progress in Optics 4 ed. by E. Wolf p. 243.